A study of the fatigue stress of concrete bridges determined by means of direct using of experimental modal data
studie únavového namáhání betonových mostů určeného pomocí přímého použití experimentálních modálních dat
Michal Polák 1
Main results of a theoretical study of fatigue stress of two concrete bridges, which is caused by moving load and which is determined by means of direct using of experimental modal data, are described in this paper. The experimentally - estimated modal parameters (frequencies, modes of natural vibration, corresponding damping values) realise the real immediate state of the observed bridge structure and its spatial behaviour. The apposite spatial model of the monitored bridge could be created directly from the experimental modal parameters of this bridge (so-called the modal model). There is possible to achieve with this model the apposite calculation of a dynamic response of an observed structure under a dynamic load. The response of the modal model under an influence of the dynamic load can be calculated by the modal decomposition method. It is possible to evaluate the response of the modal model on a stress quantity scale. The calculated time histories of the stress in given details of a structure can be processed by one of classification methods (e.g. the rain flow method). Afterwards it is possible to make the estimation of influence of the observed dynamic load on a reduction of the fatigue life of the monitored structure based on the obtained results and the Palmgren - Miner hypothesis.
Key words: Fatigue, service life, concrete bridge, experimental modal analysis, modal model.
Úvod
V článku jsou stručně popsány výsledky teoretické studie únavového namáhání dvou mostů z předpjatého betonu (mostu přes údolí Sedlického potoka na dálnici D1 v km 62,5 a mostu přes řeku Radbuzu v Plzni), které je vyvoláno dynamickými účinky pohyblivého zatížení – dopravního proudu a které bylo určeno pomocí přímého využití experimentálně určených modálních charakteristik těchto mostů. Posouzení úrovně únavového poškozování bylo provedeno podle normy pro navrhování betonových mostů [9], kde jsou uvedeny parametry Wöhlerových únavových křivek pro předpínací a betonářskou výztuž. Pro vlastní beton norma [9] Wöhlerovy křivky neuvádí.
Experimentálně určené modální charakteristiky mostu (frekvence, tvary vlastního kmitání a jim příslušný útlum) zachycují skutečný okamžitý stav sledované konstrukce a její prostorové chování v okamžiku jejího experimentálního zkoumání. Proto je lze na základě posouzení míry shody změřených a vypočtených modálních charakteristik s výhodou použít
1
Ing. Michal Polák, CSc., CTU in Prague, Faculty of Civil Engineering, Department of Structural Mechanics, Thákurova 7, Prague 6, 166 29, Czech Republic, tel.: +420/2/2435 4476, e-mail: polak@fsv.cvut.czjak k ověření výstižnosti výpočtových modelů zkoumaných mostních konstrukcí, tak i k upřesnění parametrů těchto modelů (k jejich identifikaci nebo optimalizaci). Další možností použití experimentálně určených modálních charakteristik mostu je jejich přímé využití k sestavení jeho prostorového modelu (tzv. modálního modelu). Podrobný postup se
stavení modálního modelu mostu je uveden např. v [3], [5] a také v [2]. Tento model umožňuje provést výpočet časového průběhu odezvy zkoumaného mostu na dynamické a statické zatížení. Hlavním kriteriem pro posouzení únavového poškozování mostních konstrukcí je dnes změna napětí v čase. Odezvu modálního modelu mostu na pohyblivé zatížení lze určit i v měřítku napětí. Vypočítaný časový průběh napětí v určitém vybraném detailu konstrukce (obr. 2) lze zpracovat vhodnou třídící metodou (např. metodou rain flow) (obr. 1, 2), na základě Palmgren – Minerovy hypotézy (např. [8]) a určité Wöhlerovy únavové křivky lze pak provést odhad vlivu dynamického účinku určitého zkoumaného dynamického zatížení (např. dopravního proudu) na snížení únavové životnosti sledované mostní konstrukce v posuzovaném detailu.Popis zkoumaných mostů
Na základě doporučení uvedených v
[6] byly z databanky katedry stavební mechaniky ČVUT Praha Fakulta stavební pro studii vybrány dva betonové mosty, u kterých byl k dispozici větší počet změřených tvarů vlastního kmitání zatížených malou chybou měření. U mostu v Plzni bylo k sestavení modálního modelu použito 8 tvarů vlastního kmitání, u mostu přes Sedlický potok pak 12 tvarů.Most přes řeku Radbuzu v Plzni působí staticky jako spojitý nosník o dvou polích různého rozpětí (22,6 m a 27 m). Nosnou konstrukci tvoří deska z předpjatého betonu, která je ve střední části obou polí vylehčena kruhovými otvory. Tloušťka nosné desky je 1,0 m. K provedení popisované teoretické studie byly využity tři modá
lní modely sestavené z výsledků experimentální modální analýzy provedené ve třech etapách monitorování tohoto mostu. 1.etapa monitorování se uskutečnila v dubnu 1997, 2.etapa v květnu 1998 (stav před rekonstrukcí mostu) a 3. etapa v září 2000 (stav po rekonstrukci mostu). Výsledky tohoto sledování jsou podrobně uvedeny v [4] a [7].Most přes Sedlický potok je sdružený rám o třech polích (54 + 75 + 54 m) z předpjatého betonu. Jeho nosná konstrukce je sestavena ze dvou řad segmentů komůrkového typu o konstantní výšce 4,20 m, které jsou navzájem spojené dodatečně vybetonovanou monolitickou deskou. Celková šířka mostu je 12,15 m. Popisované výpočty byly provedeny s modálními charakteristikami určenými v září 2000.
Sestavení modálního modelu mostu
Měření modálních charakteristik bylo u obou mostů uspořádáno prakticky shodně. K vyvolání kmitání byl využit budič, odezva mostu na buzení náhodnou budící sílou byla měřena induktivními snímači zrychlení B12/200 HBM. Vyhodnocení modálních parametrů z přenosových funkc
í odezvy vztažených k budící síle, bylo provedeno programem STAR (firma Spectral Dynamic). V postupu vyhodnocení vlastních tvarů je již teoreticky zohledněna jejich vzájemná ortogonalita, proto se pro potřeby sestavení modálního modelu mění pouze jejich měřítko na základě vzorce![]() , (1)
, (1)
kde {r(j)} je j-tý tvar vlastního kmitání vyhodnocený programem STAR, wd(j) je j-tá frekvence vlastního kmitání, Zss(j) je tzv. reziduum, pořadnice vlastního tvaru {r(j)} v místě působení budící síly.
Aby bylo možné na základě výpočtu provést pro vybrané detaily mostů posouzení jejich únavového namáhání, byla pro každý detail a každý změřený tvar vlastního kmitání určena na základě geometrie konstrukce a deformace vlastního tvaru v místě sledovaného detailu hodnota odpovídajícího napětí. Takto určená napětí pak byla vložena jako pořadnice jednotlivých vlastních tvarů přímo do modálního modelu. Vzhledem k chybám měření bylo nutné pořadnice vlastních tvarů vyhladit pomocí polynomických křivek prokládan
ých na základě metody nejmenších čtverců.Výpočet únavového poškození mostů vyvolaného pohyblivým zatížením
S modálním modelem lze vypočítat pouze lineární chování mostu, proto je tento model vhodný pouze ke sledování vysokocyklické únavy. Časový průběh odezvy (obr. 1) vyvolané dynamickým zatížením byl řešen pomocí rozkladu podle tvarů vlastního kmitání
[3], [5]. Vzhledem k charakteru budících sil, kterými na konstrukci působí použitý model pohyblivého zatížení, je nutné problém řešit numericky. Autor používá metodu centrálních diferencí.Pohyblivé zatížení mostu bylo v popisované studii modelováno jako dopravní proud, který byl sestavován z různě uspořádaných skupin modelů nákladních vozidel Tatra. Pro most v Plzni byly skupiny složeny z 1, 2 a 4 modelů, pro most přes Sedlický potok z 1, 4 a 6 modelů. Modely vozidel jsou sestaveny na základě metody konstrukčních prvků jako prostorové soustavy hmotných elementů navzájem propojených nehmotnými nelineárními silovými vazbami. Výstižnost takovéhoto modelování
vozidel byla ověřena již dříve.Vypočítané časové průběhy napětí (obr. 1) ve vybraných místech mostů byly zpracovány třídící metodou rain flow. Na základě získaných histogramů rozkmitů napětí (obr. 1, 2) a Palmgren – Minerovy teorie kumulace únavového poškození byl proveden odhad vlivu dynamických účinků zkoumaného seskupení nákladních vozidel na míru únavového poškození D sledované mostní konstrukce
![]() . (2)
. (2)
V rovnici (2) je ni počet cyklů napětí o rozkmitu Dsi vyvolaného pohyblivým zatížením a Ni je údaj z Wöhlerovy únavové křivky, který udává počet cyklů napětí při daném rozkmitu Dsi potřebný k únavovému poškození konstrukce. K únavovému poškození konstrukce by teoreticky nemělo dojít, pokud je D menší než 1. Hodnoty Ni z Wöhlerovy únavové křivky byly při studii převzaty z předpisu [9]. Příklady stanovené míry únavového poškození D mostu přes řeku Radbuzu od 50 přejezdů skupiny 4 nákladních vozidel jsou uvedeny v tab. 1.
Tab. 1 Hodnoty míry únavového poškození D předpínací výztuže stanovené na základě Palmgren-Minerovy teorie kumulace únavového poškození a Wöhlerovy křivky z [9] – pro 50 přejezdů skupiny čtyř nákladních vozidel různými rychlostmi v intervalu od 20 do 60 km/h - most přes řeku Radbuzu v Plzni
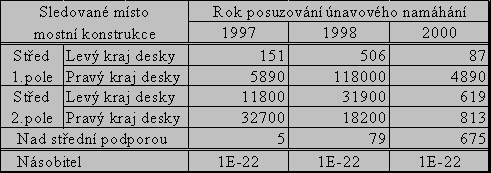
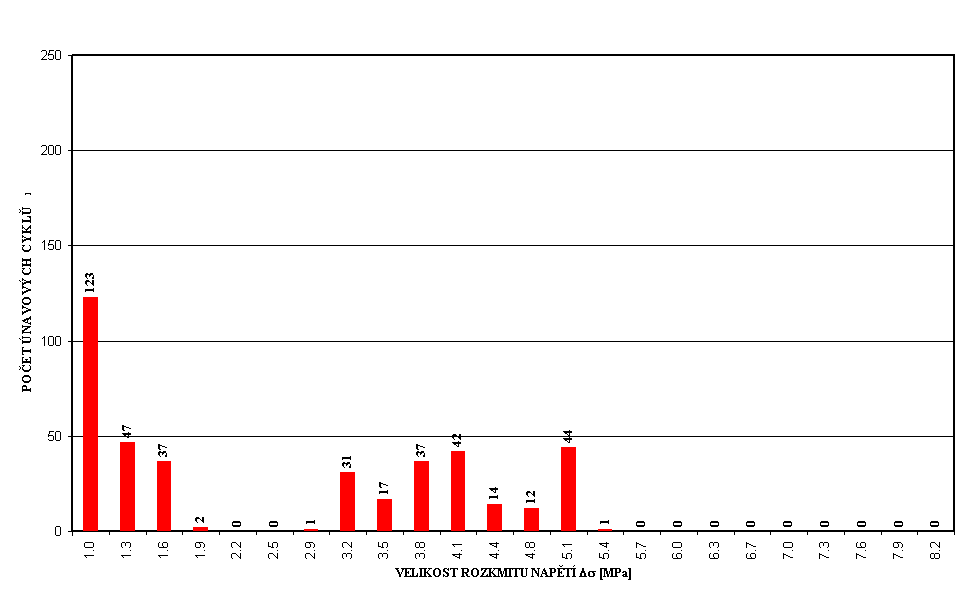
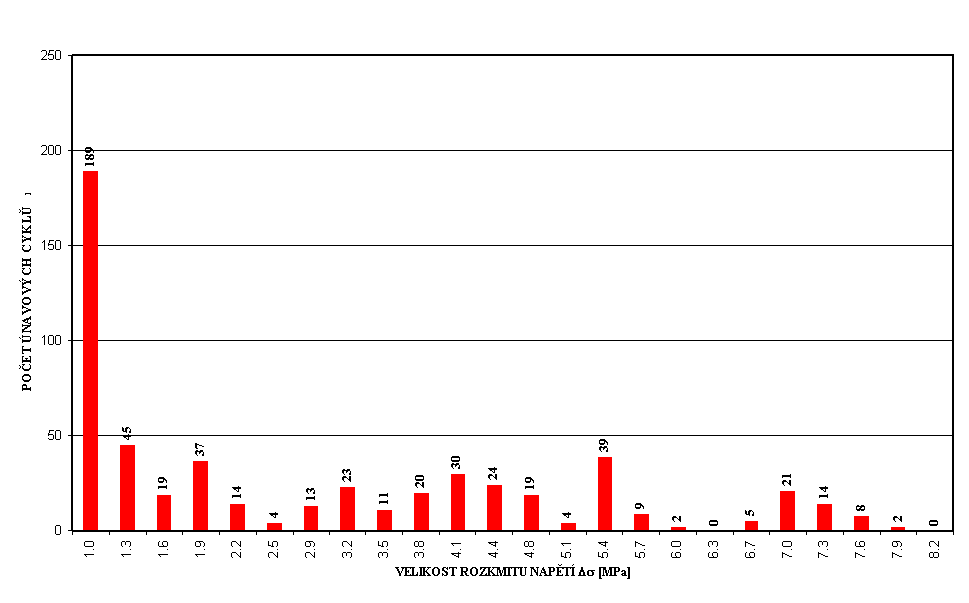
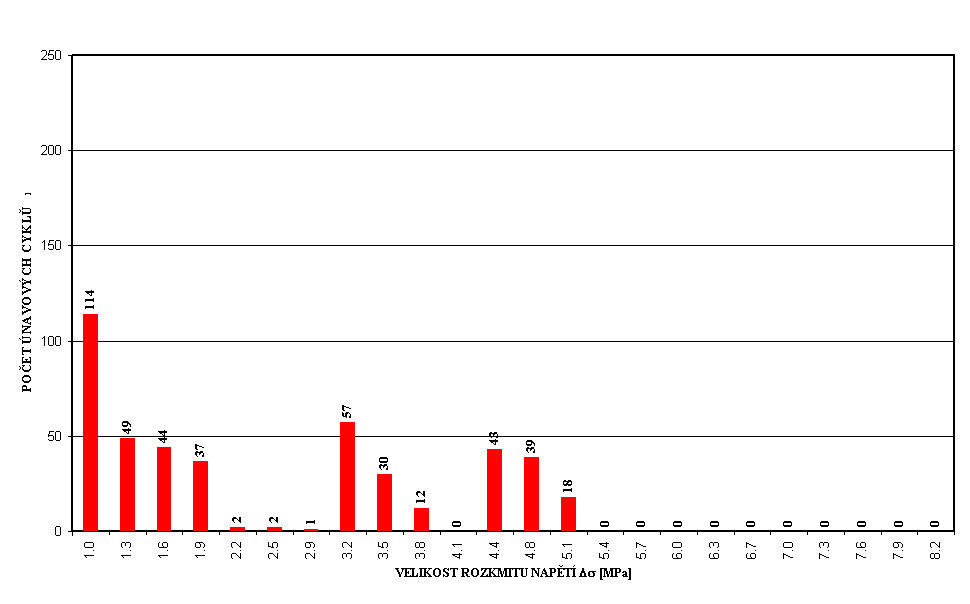
Obr. 1 Histogram rozkmitů napětí v předpínací výztuži ve středu 1.pole u pravého okraje desky pro 50 přejezdů skupiny čtyř nákladních vozidel jedoucích různými rychlostmi (v intervalu od 20 do 60 km/h) - most přes řeku Radbuzu v Plzni, rok 1997 (nahoře), rok 1998 - stav před rekonstrukcí (uprostřed), rok 2000 (stav po rekonstrukci) - střed 1.pole (kratšího) – pravý okraj desky.
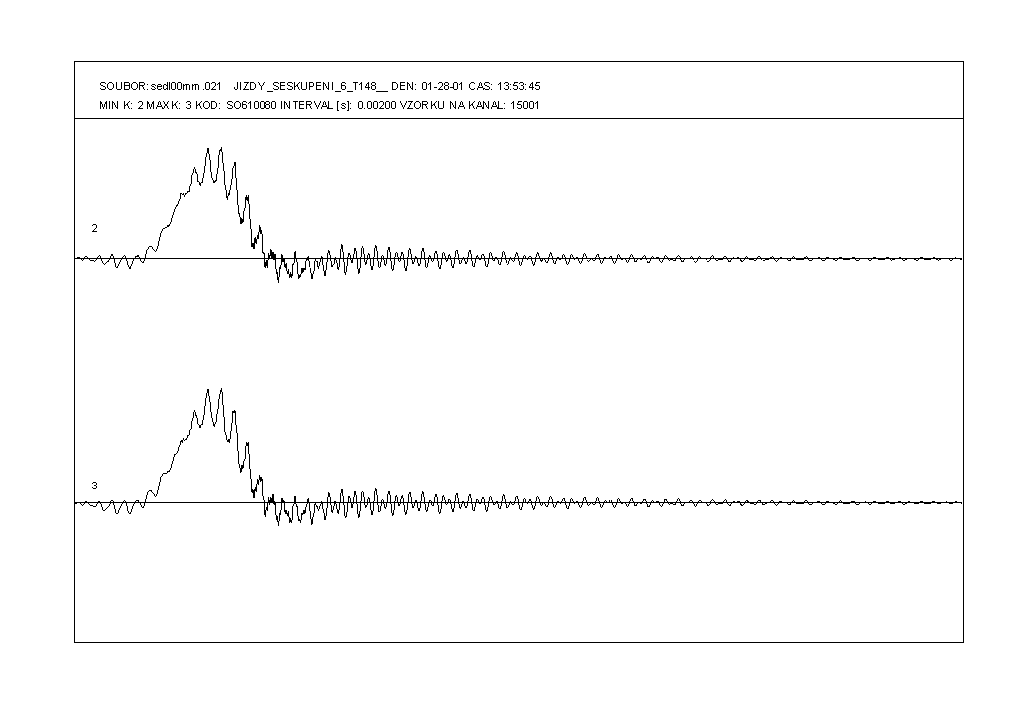
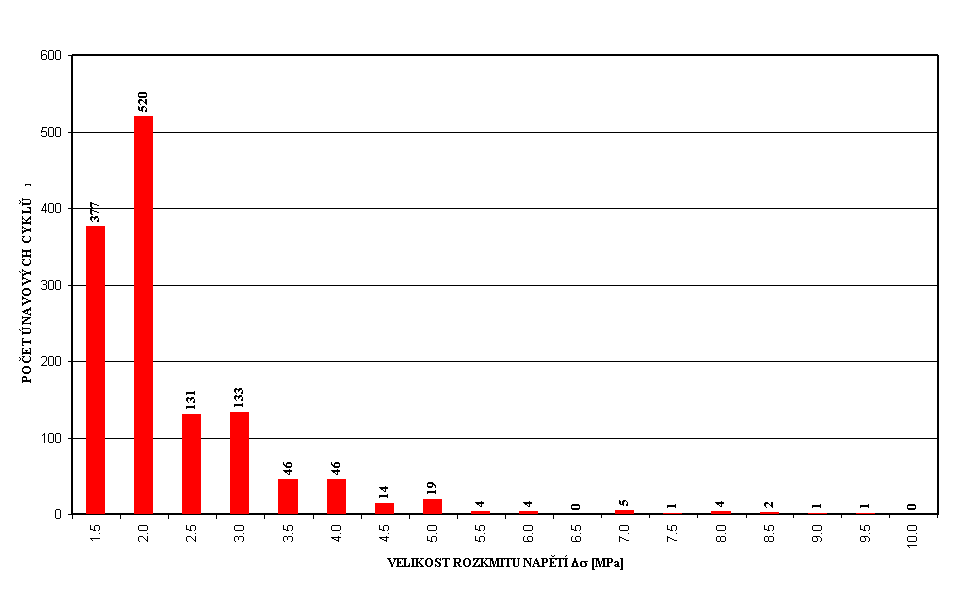
Obr. 2 Časový průběh změny napětí ve výztuži ve středu rozpětí hlavního pole mostu přes Sedlický potok při přejezdu šesti nákladních automobilů jedoucích za sebou v pravém jízdním pruhu konstantní rychlostí 70 km/h a odpovídající celkový histogram rozkmitů napětí vyvolaného 45 přejezdy shodné skupiny nákladních vozidel různými rychlostmi v intervalu od 40 do 100 km/h.
Závěr
Aby vypočítané dynamické chování zkoumaných mostů bylo co nejvýstižnější, bylo v této studii určeno s využitím prostorových modálních modelů mostů a také prostorových modelů vozidel. Toto je přínosem vzhledem k práci [2], ve které bylo pracováno pouze s rovinnými modely vozidel a rovinným modálním modelem mostu.
Výsledky studie ukazují, že míra únavového poškození D stanovená na základě normy
[9] je ve všech zkoumaných detailech obou mostů od všech použitých skupin nákladních vozidel velmi malá. Lze tedy předpokládat, že únavové namáhání vyvolané dynamickými účinky pohyblivého zatížení tyto betonové mosty během jejich plánované životnosti (cca. 100 let) neohrozí.Pro jednotlivé etapy zkoumání mostu přes řeku Radbuzu plyne (viz. tab. 1), že mezi dubnem 1997 a květnem 1998 došlo ke změně dynamického chování mostu. Toto potvrzuje i studie
[7]. Nosná konstrukce se stala citlivější na dynamické účinky pohyblivého zatížení. Po rekonstrukci mostu naopak došlo k výraznému snížení jeho únavového namáhání vyvolaného dopravním proudem.Přímé použití experimentálně určených modálních charakteristik určité mostní konstrukce k výpočtu její odezvy na dynamické a statické účinky pohyblivého zatížení je vhodná a zajímavá metoda pro zkoumání problematiky vzájemné interakce dynamického systému mostní konstrukce – pohybující se vozidla a únavového namáhání mostů vyvolaného dopravním proudem.
Tato práce byla podpořena Grantovou agenturou České republiky jako grant č. 103/96/K034 a 103/97/P108.
Literatura:
[1] Maia, N. – Silva, J. : Theoretical and Experimental Modal Analysis. Research Studies Press Ltd. Taunton, England. 1997.
[2] Molina, F.J. – Pietrzko, S. – Cantieni, R. : Direct Use of the Experimental Modal Data of a Bridge for the Prediction of its Response to a Moving Vehicle. Proceedings of Engineering Foundation Conference on Vehicle/Road and Vehicle/Bridge Interaction. Noordwijkerhout, 1994.
[3] Polák, M.: Direct use of the experimental modal data of a bridge for the calculation of its response to a dynamic load. Non-destructive Testing and Experimental Stress Analysis of Concrete Structures. Proceedings of RILEM – Imeco International Conference. Košice : Expertcentrum , 1998, pg. 369-374.
[4] Polák, M.: Study of dynamic behaviour of a prestressed concrete road bridge. Proceedings of the fourth European Conference on Structural Dynamics EURODYN’99 – Volume 2, pg.765-770, A.A.Balkema, L. Frýba & J. Náprstek editors, Rotterdam, Netherlands, 1999.
[5] Polák, M.: Výpočet únavového namáhání mostů pomocí přímého použití experimentálních modálních dat. (Evaluation of Bridge fatigue stress by means of direct using of experimental modal data.) Proceedings of the 38th International conference Experimental Stress Analysis 2000 EAN’2000, pg. 273-280, Technical University of Brno, Vlk,M.& Kotek, V. & Krejsa,J., Brno, 2000.
[6] Polák, M. - Plachý, T.: Ověření vhodnosti modálního modelu stavební konstrukce pro výpočet její únavové životnosti. Proceedings of the 38
th International conference Experimental Stress Analysis 2000 EAN’2000, pg. 263-271, Technical University of Brno, Vlk,M.& Kotek, V. & Krejsa,J., Brno, 2000.[7] Polák, M. – Sýkora, J. : Sledování změn modálních parametrů silničních mostů. Proceedings of the Int
ernational Conference on Dynamics of Civil Engineering and Transport Structures and Wind Engineering – DYN-WIND ’2000, pg. 103-106, University of Žilina, Melcer,J.& Feranec,V., Žilina, 2000.[8] Marek, P. – Guštar, M. – Bathon, L.: Tragwerkbemessung – von deterministischen zu probabilistischen verfahren. Kniha, Academia, Praha, 1998.
[9] ČSN P ENV 1992-2 : Navrhování betonových konstrukcí – Část 2: Betonové mosty. 1998